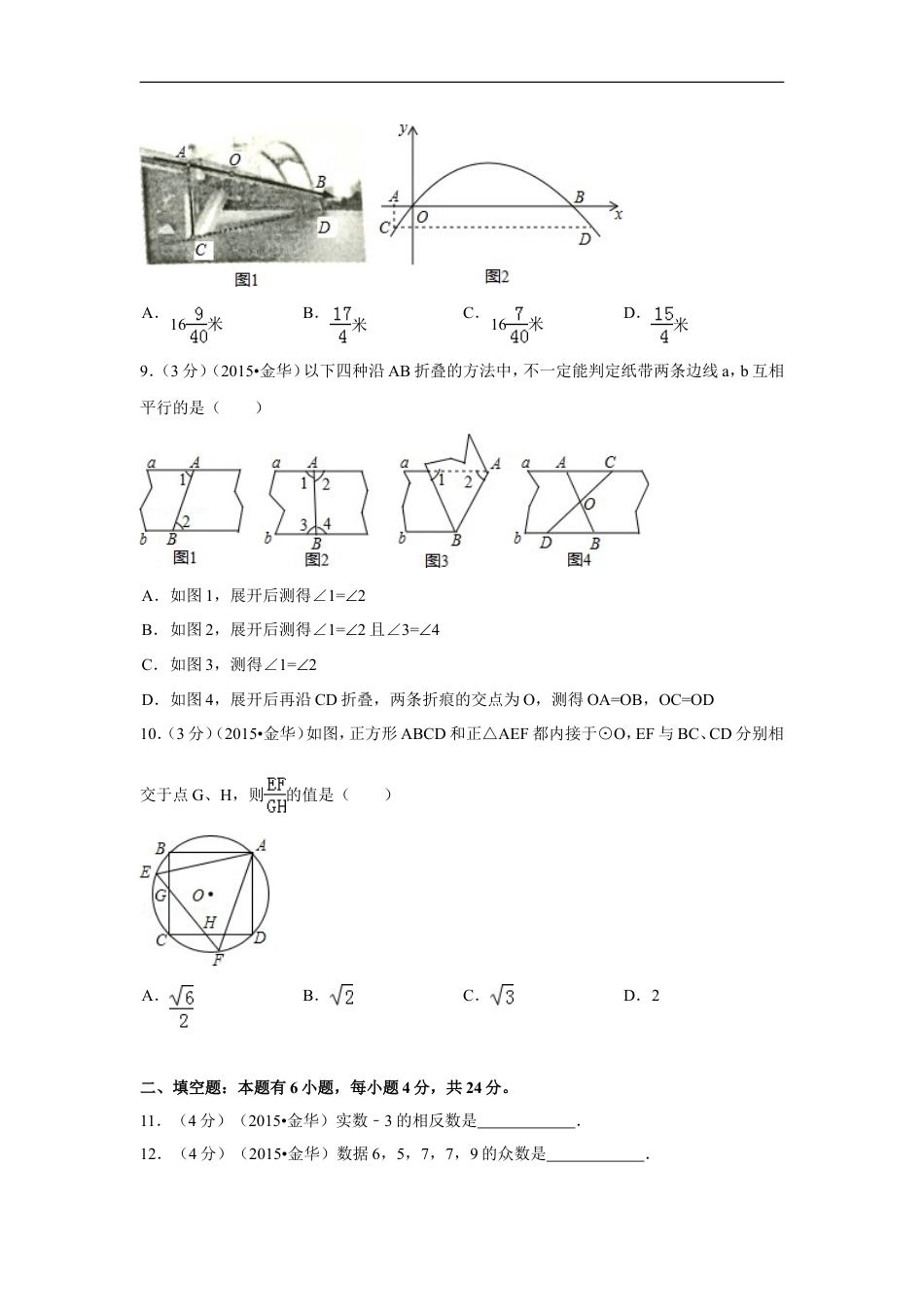
2015年浙江省金华市中考数学试卷一、选择题:本题有10小题,每小题3分,共30分。1.(3分)(2015•金华)计算(a2)3的结果是()A.a5B.a6C.a8D.3a22.(3分)(2015•金华)要使分式有意义,则x的取值应满足()A.x=2﹣B.x≠2C.x>﹣2D.x≠2﹣3.(3分)(2015•金华)点P(4,3)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限4.(3分)(2015•金华)已知∠α=35°,则∠α的补角的度数是()A.55°B.65°C.145°D.165°5.(3分)(2015•金华)一元二次方程x2+4x3=0﹣的两根为x1、x2,则x1•x2的值是()A.4B.﹣4C.3D.﹣36.(3分)(2015•金华)如图,数轴上的A、B、C、D四点中,与数﹣表示的点最接近的是()A.点AB.点BC.点CD.点D7.(3分)(2015•金华)如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是()A.B.C.D.8.(3分)(2015•金华)图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣(x80﹣)2+16,桥拱与桥墩AC的交点C恰好在水面,有ACx⊥轴,若OA=10米,则桥面离水面的高度AC为()A.16米B.米C.16米D.米9.(3分)(2015•金华)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是()A.如图1,展开后测得∠1=2∠B.如图2,展开后测得∠1=2∠且∠3=4∠C.如图3,测得∠1=2∠D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD10.(3分)(2015•金华)如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是()A.B.C.D.2二、填空题:本题有6小题,每小题4分,共24分。11.(4分)(2015•金华)实数﹣3的相反数是.12.(4分)(2015•金华)数据6,5,7,7,9的众数是.13.(4分)(2015•金华)已知a+b=3,ab=5﹣,则代数式a2b﹣2的值是.14.(4分)(2015•金华)如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是.15.(4分)(2015•金华)如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是.16.(4分)(2015•金华)图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC′D′,最后折叠形成一条线段BD″.(1)小床这样设计应用的数学原理是.(2)若AB:BC=1:4,则tanCAD∠的值是.三、解答题:本题有8小题,共66分,各小题都必须写出解答过程。17.(6分)(2015•金华)计算:.18.(6分)(2015•金华)解不等式组.19.(6分)(2015•金华)在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.20.(8分)(2015•金华)小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:(1)这次被调查的总人数是多少?(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.21.(8分)(2015•金华)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DEAF⊥,垂足为点E.(1)求证:DE=AB.(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求的长.22.(10分)(2015•金华)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为...